數學建模插值法精選(九篇)

前言：一篇好文章的誕生，需要你不斷地搜集資料、整理思路，本站小編為你收集了豐富的數學建模插值法主題范文，僅供參考，歡迎閱讀并收藏。

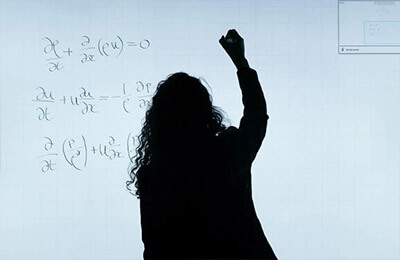
第1篇：數學建模插值法范文

【關鍵詞】數值分析；Lagrange插值法；牛頓插值法；三次樣條插值法

Collaborative Problem Teaching Method in the Research of Numerical Analysis

--Interpolation for Example

MEI Fang WANG Qiao-ling ZENG Chun-hua

（College of Science， Jiangxi Agricultural University， Nanchang Jiangxi 330045， China）

【Abstract】This paper is intended collaborative problem teaching method in the application of Numerical analysis ，creating problems，solve the problems，put forward new problems，the improved algorithm，summarizes the solving process，further more in-depth questions.

【Key words】Numerical analysis；Lagrange interpolation；Newton interpolation；Cubic spline interpolation

問題驅動式教學法是基于問題的教學方法，一種建立在構建主義教學理論基礎上的教學法，它要求“問題”的目標性和教學情景的創建，學生在老師的幫助下，緊緊圍繞共同的任務，在強烈的真實問題動機的驅動下，通過對資源的積極主動應用，進行自主探索和互動協作的學習。

目前國內大學《數值分析》課程的教學改革起步晚，注重純理論教學。教學過程中存在的不足：數學理論推導嚴密但是教學枯燥，學生學習缺乏興趣。國外《數值分析》課程的改革走在前沿，美國工程院院士Cleve Moler在20世紀70年代提出在學習方式上，將教師引導與學生自主探究、合作交流有機結合起來。注意吸收計算數學中算法研究的最新理論研究成果，讓學生在真實的問題驅動下，帶著問題去學習領會蘊含其中的算法原理，并能運用所學理論分析利用數學軟件解決現實生活中的科學問題。但對驅動問題的解決措施的探討深入不夠。

本文以數值分析課程的插值法為例，介紹問題驅動式教學法在整個章節課堂教學中的研究與應用。

1 創設問題情境，提出問題

函數是描述自然界客觀規律的重要工具，實際應用中許多函數是通過實驗或者觀測得到的，其形式是一張函數表，作一條曲線，其類型（代數多項式函數，三角函數，指數函數……）是事先人為給定的，該曲線經過所有點（xi，yi），i=0，1，2，…，n，這就是所謂的插值問題。

據資料記載，某地某年間隔30天的日落時間如下：

根據上述資料，計算這一年中哪一天白天“最長”。

2 引導學生討論交流，解決問題

讓學生查找資料，分組討論，了解插值法的產生背景，中外數學家在此問題上研究的進程，這種古老的分析問題數學方法應用在那些課題中？分析關于多項式插值的理論依據是什么？提出問題對于函數y=f（x）是否存在這樣的多項式函數P（x）能精確的逼近它呢？經過數學的推導得到結論：滿足給定區間[a，b]上n+1個點a≤x0

然后得到Lagrange插值法的計算公式：

■（1）

其中

■（2）

插值余項與誤差估計：

■（3）

■（4）

其中■（5）

接下來，按上面的理論知識，求解提出的問題，建立一個簡單的數學模型，用二次等距離插值法計算求解：

5月1日設為第0天，則x=0

再設每一天白天的長度（日出與日落的時數）為14小時13分+T分

故天數和它的長度可用（x，T）表示。有記載的三天數據對應于（0，0），（30，68），（60，81）

將它們帶入Lagrange插值公式得白天的時長：T=■，

由微積分中的最值原理T'（x）=0，得到x≈52.09，

也就是最長的一天為5月1日以后的第52天，即6月22日，T=83分，這一天日出與日落之間的時數為14小時13分+83分=15小時36分。與每年的夏至節氣日期相吻合。

然后拓展數值分析插值法數學實驗，計算一年中的24節氣所在的具體日期。

3 解決問題的基礎上，進一步了解插值法在理論和實踐上發展，應用的廣泛性，提出新問題和知識延拓

Lagrange 插值公式結構緊湊，思路清晰，程序編制容易，但是增減節點時，計算要全部重新計算，很不方便，增加計算量，我們希望在增加新的節點時，原先計算的結果對后來的計算過程仍然有用，那如何改進？于是我們得到Newton插值多項式

■（6）

余項■（7）

其中ωn+1（x）由（5）式定義。

插值多項式要求插值節點相等，而實際問題中還經常要求節點上的導數值相等，甚至高階導數值也相等，于是課題條件改變了，我們討論新的解決問題的方法Hermite插值法。這類型的一般問題顯然會具有些令人感興趣的困難，在稱為伯格霍夫插值的專題中奉獻了大量的近期研究文獻，學生可以查閱。

其它的插值法，早期的板材曲線切割時，常常把富有彈性的細長木條（樣條）固定在樣點上，比方說航空造船等工程設計的需要，要求樣條曲線二階導數連續，三次樣條函數插值是被認為一種有效的數學工具，并且學生將看到，插值法的算法有很多種，針對問題選擇方法十分關鍵，正確選擇算法的前提是對方法的理解、分析、評價和鑒賞。

4 歸納解決問題中的知識點，強化系統認知能力，完善問題的結論，總結規律，提出更深一步的問題

插值法是一個古老而實用的方法，作為逼近函數的構造方法，是數值微積分，函數逼近，微分方程數值解的基礎。因為高次插值的Runge現象，隨著信息量的增加，實驗的結果與直觀的想象不吻合，它也是數值計算研究中值得高度重視的一類現象，也就是說Lagrange插值多項式的次數不可能無限制的增大，所以它沒有實用性，采用分段低次插值，特別是三次樣條插值，具有良好的收斂性與穩定性，理論上和應用上意義重要，在計算機圖形學中有重要應用。

數值分析是研究用數學方法處理信息的學科，僅僅是實用信息量大，如果使用方法不當，也不能保證所得結果的正確性，在教學過程中提出一種知識建模化的問題驅動式教學方法，把學生在現實生活中感興趣的相關問題，引入數值分析算法的教學之中，將問題驅動與數值分析的各種算法技術相結合，加深對《數值分析》這門課程的有關算法和結論的理解，激發學生積極思考和避免一些常犯易犯的錯誤，提出一種實用有效的問題驅動的教學內容結構設計，打破傳統的教學模式，讓數值分析的學習更高效。

【參考文獻】

[1]李慶揚，王超能，易大義.數值分析[M].5版.北京：清華大學出版社，2008：22-46.

[2]林成森.數值分析[M].2版.北京：科學出版社，2005：114-190.

[3]白峰杉.數值分析引論[M].2版.北京：高等教育出版社，2010：92-104.

[4]任玉杰.數值分析及其MATLAB實現[M].北京：高等教育出版社，2008：354-480.

第2篇：數學建模插值法范文

[關鍵詞] 中心性漿液性脈絡膜視網膜病變 疏肝健脾活血利水法

[中圖分類號] R242[文獻標識碼] A[文章編號] 1005-0515（2011）-08-133-01

中心性漿液性脈絡膜視網膜病變，是一種病因和發病機制尚未完全清楚的眼底病變，簡稱“中漿”病[1]。癥狀表現為視網膜色素上皮屏障功能失常,形成黃斑部視網膜神經上皮淺脫離，致視力減退、視物變形和視覺變暗。好發于20-45歲的青壯年男性，多單眼發病。盡管該病有自限性，但病程較長，部分病例反復發作或遷延不愈，造成視力功能損害。目前，尚無特殊藥物治療。筆者觀察采用疏肝健脾活血利水中藥治療40例(44眼),與同時采用常規西藥治療40例(42眼)進行對比，發現療效滿意,現報道如下。

1 診斷與臨床資料

1.1 診斷標準 參照《眼科學》[2] ①視力減退或模糊，視物變形、變小、變色等；②外眼檢查正常；③眼底檢查黃斑區水腫，呈圓形或橢圓形的反光環，中心凹光反射消失，黃斑區可見細小黃白色點狀滲出物；④眼底熒光素血管造影檢查在黃斑區可見熒光素滲漏現象。

1.2 篩選對象 ①符合上述診斷標準；②發病均在1個月以內，未經治療初次發病的中漿病患者,均無全身和眼部其他病癥；③眼底熒光素滲漏點分布位置均離黃斑中心凹250um以外,非孕期婦女。

1.3 一般資料 觀察病例共80例(86眼),均為眼科2004年1月-2008年1月門診確診“中漿”的患者。按數字表法隨機分為2組。治療組40例44眼，男35例38眼，女5例6眼，年齡38.4±7.5歲；對照組40例42眼，男37例39眼，女3例3眼,年齡35.4±7.6歲，眼底血管熒光造影均發現1處以上熒光素滲漏點。兩組患者在年齡、病程、病眼遠視力方面經t檢驗,眼底滲漏點分布位置及黃斑水腫程度方面經X2檢驗，比較差異均無統計學意義(P>0.05)，具有可比性。

2 方法

2.1 治療組 患者服用疏肝健脾活血利水中藥，基本藥方：柴胡10g、當歸10g、白芍10g、黃芪30g、白術10g、茯苓10g、車前子10g、赤芍10g、紅花6g。隨癥加減用藥，水腫明顯加益母草15g,滲出較多加田三七10g，視力恢復較慢者加桑椹子10g。每日1劑，分別水煎2次，混合后分早晚2次服用。

2.2 對照組 患者使用常規西藥治療，每次口服維生素B1片10mg，維生素E膠丸0.1g，三磷酸腺苷片40mg,肌苷片0.4g，一天3次。

2.3 治療時間 兩組均治療2周為一療程，各觀察6周。

3 觀察項目與統計方法

3.1 觀察項目 ①采用國際標準視力表檢查，有屈光不正者在自動計算機驗光儀電腦驗光基礎上，結合人工檢影插片，以獲得最佳矯正視力。每療程前后記錄1次。②眼底每療程檢查1次。③熒光眼底造影治療前后各1次。④全部病例6周后追蹤觀察1年。

3.2 統計方法 采用SPSS14.0統計軟件進行數據處理，計量資料用均數±標準差(x±S)表示,采用成組t檢驗；計數資料采用X2檢驗；等級資料采用秩和檢驗。檢驗水準為0.05。

4 療效標準與治療結果

4.1 療效標準 參考《中醫病證診斷療效標準》[3]治愈：黃斑區蛋白沉著物完全吸收，色素沉著完全消退，黃斑中心凹光反射出現，黃斑結構恢復正常，視力達1.0以上,熒光造影無滲漏者。顯效：黃斑區蛋白沉著物完全吸收，但仍有不同程度的色素沉著存在，黃斑中心凹光反射出視，視力達0.8,熒光滲漏有縮小或減少者。有效：黃斑區蛋白沉著物未完全吸收，遺留機化物變性灶與較多的色素沉著，視力提高1～2行, 熒光滲漏有縮小或減少者。無效：眼底情況無改善，視力未提高或下降, 熒光滲漏未改善者。總有效率以治愈加顯效、有效計。

4.2 治療結果 治療組黃斑區蛋白沉著物與色素沉著物的吸收情況均優于對照組(P

表1兩組治療后眼底變化比較(例)

注: 治療組對照組黃斑區蛋白沉著物比較，Z＝－2.016，P＜0.05；治療組對照組黃斑區色素沉著物比較，Z＝－2.125，P＜0.05。

表2兩組治療前后視力比較(x±S)

注:治療組治療前后比較,t＝－12.603 ,P＜0.01；對照組治療前后比較,t＝－6.193 ,P＜0.01；治療組對照組治療前比較,t=-0.158 ,P＞0.05,治療后比較,t=5.621 ,P＜0.01。

表3 兩組治療后眼底造影熒光素滲漏情況比較（例）

注：兩組比較，Z＝－2.203，P＜0.05。

表4 兩組療效比較（例）

注：兩組比較，Z＝－2.393，P＜0.05。

4.3 隨訪結果 治療組40例(44眼)中,有4例(4眼)經4-12月隨訪后失去聯系,對照組40例(42眼)中,有5例(6眼)經6-12月隨訪后失去聯系,未予統計。兩組復發率比較,差異有統計學意義(P

表5 兩組隨訪結果比較(例)

注：兩組比較，X2＝9.935，P＜0.01。

5 討論

5.1 有報道稱，“中漿”病與腎功能衰竭、感染、中毒、過敏、精神緊張、壓力大、情緒波動、勞倦和使用皮質類固醇等綜合因素有關[4]，引發人體植物神經功能失調，局部微循環紊亂，致視網膜色素上皮層封閉小帶的局限性損害，而使其屏障功能受到破壞。

5.2 患者如滲漏點距黃斑中心凹250um以外，可采用激光治療以縮短病程[5-7]，但不能阻止、減少或預防復發[4]，對于持續視網膜下滲液積聚的慢性、嚴重的復發病例，作用局限。隨著中醫發展研究，中醫療效顯著病例不斷增多[8-11]，人們越來越重視使用活血化瘀的中藥，促進滲漏吸收、加快恢復視力、縮短病程并預防和減少復發，又可避免激光光凝可能導致的視網膜功能損傷，彌補了激光治療的不足。

5.3 “中漿”病臨床上以黃斑部水腫、滲出為主要病理表現，屬中醫“視瞻昏渺”、“視瞻有色”、“視直如曲”的內障眼病范疇[12]。中醫學認為，目之視物辨色功能與肝氣密切相關，“肝氣通于目，肝和則目能辨五色矣”(《靈樞?脈度》)。同時根據五輪學說及近代醫家陳達夫教授六經辨證的觀點，視網膜屬肝，位于視網膜中央之黃斑屬脾,黃斑病變與脾的運化功能失調密切相關。若肝失疏泄, 肝郁犯脾，脾失健運，水濕上犯目竅，日久聚濕生痰,痰濕阻滯脈絡，導致本病發生。因此，治當遵循“疏肝健脾,利水活血”之則。方中柴胡疏肝解郁,配當歸、白芍養血柔肝，而使肝氣條達舒暢；黃芪、白術、茯苓、車前子健脾利濕；赤芍、紅花、地龍則活血化瘀。諸藥合用,使肝氣疏，脾健運，水濕瘀盡去,諸癥可愈。

治療組采用疏肝健脾活血利水法治療“中漿”病，與對照組比較,能促進黃斑區蛋白沉著物的吸收和黃斑區色素沉著物的消退, 眼底造影熒光素無滲漏或減少滲漏, 明顯提高視力,預防和減少復發，療效滿意。故疏肝健脾活血利水法是治療中心性漿液性脈絡膜視網膜病變的有效方法，值得推廣。

參考文獻

[1] 劉家琦,李鳳鳴.實用眼科學[M].北京:人民衛生出版社,2002:495.

[2] 黃叔仁,張曉峰.眼底病診斷與治療[M].北京:人民衛生出版社,2003:228.

[3] 國家中醫藥管理局.中醫病癥診斷療效標準[S].南京:南京大學出版社,1994:110.

[4] 向圣錦,林穎,劉安.中心性漿液性脈絡膜視網膜病變的中西醫研究現狀[J].中國中醫眼科雜志,2006,16(1):57-59.

[5] 何劍峰.激光治療中心性漿液性脈絡膜視網膜病變228例[J].國際眼科雜志,2004,4(1):165-167.

[6] 鄭秀云,蘇艷,劉素美,等.氬激光治療中心性漿液性脈絡膜視網膜病變730例臨床分析[J].臨床眼科雜志,2001,9(6):460-461.

[7] 劉釗臣,李銳.532激光治療中心性漿液性脈絡膜視網膜病變的療效觀察[J].國際眼科雜志,2009,9(12):2451-2452.

[8] 劉建勇.中心性漿液性脈絡膜視網膜病變的中醫治療近況[J].浙江中醫雜志,2002,10:45.

[9] 劉敬良,郵太玲,丕華,等.辨證治療中心性漿液性脈絡膜視網膜病變64例[J].實用中醫藥雜志,2004,20(7):369.

[10] 薛尚才.中心性漿液性脈絡膜視網膜病變的中醫分型、分期治療[J].中國實用眼科雜志,2004,22(3):233.

第3篇：數學建模插值法范文

關鍵詞： 數值計算課程 科學計算 教學方法

理論推演與實驗證明是傳統的兩大科學方法。隨著計算機的發展及其在科學技術領域的應用、推廣與深化，科學計算已成為繼理論推演和實驗證明之外的第三種科學手段。現在，作為科學計算基礎內容的數值計算方法已被廣泛應用于科學技術和國民經濟的各個領域，如石油的勘探與開發、大型水利工程的設計與建筑、天氣預報等。數值計算方法之所以應用廣泛，一方面因為計算方法是實際問題數值模擬方法的設計、分析與軟件實現的理論基礎，其內容涉及數學、物理、力學、化學、計算機科學等多種學科的有關內容，另一方面，計算機的發展使得計算方法有了先進的計算工具，而計算能力的提高又使得數值計算成為現實。數值計算是一門介紹適用于計算機上使用的數值分析方法的課程，也稱為計算方法課程。數值計算課程是科學計算的基礎和理論保障，是大學工科數學中的一門重要課程。

一、數值計算課程的特點

數值計算方法的基礎是高等數學、線性代數等課程。數值計算是以數學問題為研究對象的一門學科，具有完善的理論體系，它雖然是數學的一個分支，但不同于純數學那樣只研究數學理論本身，而是著重研究求數學問題的各種數值計算方法和相關理論，包括方法的收斂性、穩定性、誤差分析等，為數學問題依靠計算機來求解提供有效的數值方法。為了使學生能夠更好地掌握數值計算課程的基本思想、基本原理和基本方法，教師要擺脫數學思維模式的束縛，過渡到數值思想，提高學生的科學計算的素質。

數值計算課程內容主要包括：數值逼近、數值代數、微分方程數值解法等。它具有以下幾個特點。

1.實用性。這門課程中的許多方法的理論基礎是在高等數學和線性代數中學習過的知識，但是與這些基礎課程強調理論分析不同，它更注重運用這些理論分析的結果，同時它注重應用的科學性，注重解決實際問題。

2.注重算法。數值計算課程主要研究算法，算法必須能在計算機上實現。例如，解一個含有大量未知量的線性方程組或計算高階矩陣的全部特征根，無論計算方法如何好，單憑人工都是很難實現的。這就要求我們會利用計算機進行編程計算，或利用現成的軟件進行計算，這無疑對學生的計算機水平提出了相當高的要求。另外很多計算方法都具有便于計算機求解的特點。

3.工程背景強。數值計算方法中的數學方法和理論，本身并不都是數學學科的產物，它首先來源于實際計算的需要，該課程十分注重解決實際工程問題，在地質勘探、汽車制造、天氣預報、航空航天技術中已經得到廣泛的運用，它是解決“計算”問題的橋梁和工具。

二、學生科學計算素質應包括的內容

數值計算方法中蘊含著豐富的數學思想和數學方法，在教學中應注意由淺入深、由特殊到一般，在介紹方法和引進概念時應力求揭示問題的實質，對于方法和概念之間應著重闡明其聯系。數值計算方法中有如下一些常用的方法，它們應該是提高學生科學計算素質的重要內容：

1.遞推法。遞推法是計算公式中常采用的形式，它的基本思想是將一個復雜的計算過程歸結為簡單過程的多次重復，這種重復在算法中表現為循環。例如多項式求值的秦九韶方法，就是通過一次式的反復計算，逐步得出高次多項式的值，這種化繁為簡的方法是計算方法研究的基本原則之一。

2.迭代法。迭代法是處理線性或非線性問題的重要手段之一。迭代法是指按同一公式重復計算的一個數值過程。例如用雅克比迭代法和賽德爾迭代法求線性方程組的數值解，就是先構造迭代公式，再選定初值，逐次計算，得到近似解。

3.以直代曲。這是計算方法常用的手段之一，它的思路是將非線性問題線性化，即在局部范圍內用直線近似代替曲線。例如用牛頓迭代法求非線性方程的解，就是典型的以直代曲的例子。

4.化整為零也是計算方法研究的一種重要手段。用復化梯形公式和復合辛普森公式求定積分的近似值就是一個典型的例子。

遞推法、迭代法、局部以直代曲法、化整為零法，在計算方法的研究中常常互相滲透、互相聯系。如牛頓法解非線性方程是局部以直代曲和迭代法的結合，復合梯形公式求定積分是化整為零和局部以直代曲的結合。這些方法都是用極限思想研究不同數值問題的具體表現。極限思想是從有限中找到無限，并且使之確定下來的一種思想。解非線性方程的牛頓法是一個迭代過程，是極限無限變化過程中的某個階段，一方面計算機快速而有效的計算可以完成這個階段，給出計算結果的數值表，另一方面分析此數值表能夠幫助我們判斷此算法的收斂性和收斂的快慢程度。當然我們還可以用極限的思想構造其他解非線性方程的數值解法，并分析每一種數值方法的實用性和有效性。極限思想在計算方法中的應用，使學生對極限的概念有了更直觀和深刻的理解，從而提高了學生的科學計算的素質。

三、加強數值計算方法課程的教學與考核

為提高學生的科學計算素質，就要加強該課程的教學和考核工作。首先要制定適當的教學大綱與考試大綱，其次要通過改革教學方法及方式，培養學生應用數學解決問題的能力，使學生能夠把所學內容有機地結合在一起，形成一個完整的理論體系，從而激發學生的學習興趣，培養他們的創新精神。

1.課堂教學。課堂講授是數值計算方法教學中的主要部分，我們應該盡可能地突出數值計算課程的特色。由于數值計算中涉及的問題都是從實際中提煉出來的，再應用數學的理論加以推導，最后提出具體的解決方法，因此，每種數值方法的講授都應該盡量地從實例中提出問題，引導學生去思考如何運用數學知識去構造解決的方法，然后再給出相應的數學理論。實際上，數值分析的教學過程恰好就是一個簡單的科學研究過程，這種教學方法能夠激發學生的學習興趣，使學生對知識的掌握更加扎實。

目前在數值計算教學中還存在一些普遍的問題，如：教學課時有限，課堂講授不可能面面俱到；覆蓋的知識面寬，各部分內容自成體系，結構松散，前后連貫性不強；對問題實際背景分析不夠，不了解數學思維過程，很難激發學生的學習興趣，學生的實踐能力也不強；一般教材對實驗指導方面不夠重視，不利于提高學生的應用能力。為解決這些問題，應該對教材內容進行必要的選擇，進行必要的加工。例如常微分方程的數值解，不僅要學習初值問題，而且對邊值問題也要進行適當的討論，以適應數學建模的廣泛性，使講授的內容不僅具有適用性，而且具有嚴密的邏輯性和完整性。

多年延續下來的授課方式大多是板書，對課本內容邊講解、邊板書而完成。現代數值計算方法信息量大、公式繁多、理論與實際結合強，采用傳統方式教學，黑板板書占用了大量時間，不利于豐富課堂教學內容，也無法向學生進行程序演示與算法比較，所以我們要對教學方法及教學手段進行改革。數值分析的知識由許多不同的部分組成，而且內容十分廣泛，授課時，先從它的實際背景入手，分析建立數學模型的思路及計算方法的理論依據，努力使各部分之間保持緊密的聯系，引導學生找出各知識點之間的關系，以及它們的不同之處，分析各種計算方法，提出它們的缺點所在，例如方法的收斂性和穩定性，以及是否為病態問題，這樣學生的思路就會非常清晰。例如在插值法的教學中，首先用嚴密的數學推理解決插值多項式解的存在唯一性，然后對表達式進行求解，從而得到拉格朗日插值法，再通過理論分析，引出牛頓插值法、赫米特插值法等，直至三次樣條插值，這樣就形成一個完整的插值計算法。在教學中，要適當地運用現代化手段。由于數值計算的理論基礎就是數學，它的理論推導有時比較復雜，但原理并不抽象。如果我們只是推導演算來求得計算公式，不但會把一個簡單公式復雜化，而且勢必會分散學生的注意力，讓他們感到枯燥無味，使其在情緒上產生抵觸心理，降低學習效率。利用多媒體輔助教學，可以增大信息量，節省一些不必要的時間，把精力集中在講透基本概念、基本原理及算法實現上，再把一部分實例圖形展示給學生，會加深他們的印象與理解。還可以分步重復演示，有效地強化課堂教學效果，激發學生對問題的直觀認識，有利于培養學生的創造性思維能力，因而多媒體課件輔助教學也是教學改革的一個重要內容。

2.實驗教學。數值計算是一門實驗性學科。如果我們只講授一些算法，不去上機實際操作，勢必會造成學生的實踐與應用能力很差，學到的知識除了應付考試外不知道如何使用和有什么實際用途。此外，上機實驗不但能培養學生的實踐能力，而且對其編程能力也有所提高。由于計算方法不但要求適合于計算機上使用，而且該算法必須具有算法的穩定性、理論的可靠性及計算的復雜性，因而上機實踐是必不可少的。這也是一個消化所學內容的過程，以此來驗證各種方法的優缺點，同時也是改進編寫計算機程序的過程，通過自己的親自編程實踐來解決一些簡單的實際問題，也是充分調動學生參與的過程，使學生做到學有所用。這樣不僅能使學生掌握計算方法的理論知識，學會解決一些簡單問題的方法，更重要的是使學生能體會數學的用處。近幾年來全國大學生數學建模比賽，更是體現了利用數學思想提煉出解決一些實際問題的數學模型，然后從理論上進行分析研究，最后編制實驗程序、上機實踐，使得問題得以解決。上機課的目的主要在于培養學生的實踐和編程能力，將課堂上學到的數值分析方法理論應用到具體的實例中，這是一個消化課堂上學習的知識點的過程。學生針對同一個問題可以嘗試不同方法去解決，并且加以比較，以此來驗證各種方法的優缺點。數值分析中的問題僅靠課堂教學、理論推導是很難講明白的，例如收斂性、穩定性等相關問題，學生在實際的計算過程中，可以通過畫圖或列表等比較的方式對課堂的知識加深理解。上機實驗與課堂教學的結合也是一種初級科研過程，讓學生初步感受到科研的樂趣、困難及氣氛。但是需要說明的是，上機實驗這一教學環節也存在著一些問題：實習題目重復與學生之間的抄襲問題。教師可以將學生分組做不同的題目，或者針對同一題目，應用多種方法選擇不同的參數求解，然后比較它們之間的差別。上機實驗部分的教學仍有許多需要改進之處，為保證上機質量，在每次上機之前均布置上機作業，并要求學生按上機目的、算法原理、程序、計算結果及結果分析寫出上機報告。實踐證明，上機實踐調動了學生的學習積極性，有利于發揮學生的主觀能動性，同時也提高了學生的動手能力。

3.考核檢查。考核是每門課程的最后一個環節。以前，數值計算方法課程考試為筆試，其成績由期中、期末成績按比例計算。這樣的考核方式雖然簡單、易于操作，但這也是學生不重視實驗、不注重如何應用所學知識解決實際問題的原因之一，造成了學生理論聯系實際和解決實際問題的能力差。針對數值分析課程的特點，除平時成績之外，應將數值實驗放在考核范圍之內，上機書面報告是考核內容之一。作業是考核內容之一，教師要精選一些與教學內容相聯系的習題，注重鞏固提高學生的基礎知識，使學生掌握基本技能和技巧，獲得一些解題方法。做作業是學生學習數學的必要手段之一，很多知識需要整理、推導、應用，才能從中理解所學內容。實驗考核是考核的一部分，上機要有實驗報告，為避免學生應付或抄襲，應分組實驗，每組所給數據（原始）稍做改動，引導學生重視理論和實踐相結合，激發他們的創作熱情，培養學生積極向上的精神。要重視書面考核的設計，力求知識面廣、題型內容豐富，既考查基礎知識，又考查解決問題的能力，促進教學的良性循環。

參考文獻：

［1］李慶楊，王能超，易大義.數值分析［M］.武漢：華中科技大學出版社，2001.

第4篇：數學建模插值法范文

關鍵詞：有限元；足部；跖骨；趾骨；脛骨；腓骨

一直以來，國內外都有大量飽受足部病痛的患者。在這之中，超過七成的病痛都是足底筋膜炎和腱膜炎導致的。[1] 國外現有的治療方法，是由醫生用患者踩踏軟泥得到的腳型，澆注成模，再制造出完全貼合腳型的鞋子，來頂起足弓處，分擔受力，使筋膜、腱膜緩慢康復。但此制鞋過程需耗費一個月時間、且價格昂貴。[2] 于是，全新的制鞋理念誕生：在鞋內加入剛度和高度調節裝置，配合貼合腳底特征的鞋墊即可。為了更好地設計與落實此理念，需要對腳部進行有限元分析，建立腳部模型，施加受力和位置限制，了解足部各處的受力分布，從而確定兩調節器的放設位置。同時，也可為醫生治療提供更科學的受力分析情況。

一、現有模型的問題

為了得到腳部模型，需要依次實行如下步驟：用3D掃描儀得到腳部特征，將其修復改進成點云集合，導成有限元軟件可以導入的模型格式，并且利用線性或非線性數學原理增加節點數，以填滿所有點云間的空隙。[3]

在過程中的最后一步，建模人員總共需要設置八萬五千個節點來建模，工作量十分巨大。而且為了確保精確性，更好的方法是在inp文件中手動修改。[4] 縱然節點的坐標可以在其他軟件中由程序得到，一來一回的操作也是十分復雜。這其中稍有運算上的漏洞，就要推倒重來。更為復雜的是，建模的下一步，是要模擬軟骨和韌帶。兩者分布在腳上，可以用設置單元，將兩節點連接起來的方式來得到。但為了確保精確性，研究人員需要仔細研讀解剖學的書，找出八萬個節點中精確的兩點，顯然非常費時費力。以上的步驟，對每一個患者，都要再來一次，工作量可見一斑。雖然不需醫生花一個月時間進行手工制作，但作為此創意鞋的先行步驟，有限元分析的建模就要耗費如此精力，對醫生而言，不切實際也無法憑自己能力完成，不利于鞋子的下一步推廣。

二、解決方案

（一）基本概念和簡化方法

最主要的方法是將五根趾骨和五根跖骨進行線性化替代。顯然的是，軟骨和韌帶都是由代表肉質的兩個節點連接而成，與骨頭所代表的節點并無關聯，故進行線性化，減少的節點不會對受力分析的結果有直接影響。其二，五根趾骨和五根跖骨在自身的整個長度中除了截面面積的變化外，別的性質，例如骨頭密度、楊氏模量都未發生變化；慣量、轉動慣量則都是隨截面面積這一自變量進行變化。故只要在線性化的過程中體現出截面面積的變化，即可大致進行等量轉換。[5]

值得注意的是，在跖骨和趾骨交界處的籽骨，必須予以保留。借此，兩骨與腳部整體的相對性得以保留。當脛骨和腓骨所受的力向下傳遞至腳跟及腳后部的骰骨、舟骨、跟骨、距骨時，五根跖骨因為都與四骨之一及籽骨之間連接，受力情況可保持與簡化前模型相同。[6] 另外，跖骨和趾骨分別用兩個方向的彈簧和籽骨相連，模擬出平動和轉動兩種相對位置的變化。

第二個可以簡化的是最上端的脛骨和腓骨。許多同領域的前期研究，都基本一致得認為分析受力，需要保留整個腳部直至脛骨和腓骨--腳踝處的距骨與腓骨、脛骨、舟骨都通過軟骨有接觸，此處受力最為復雜，故必須集體保留腓骨和脛骨才能得到準確結果。[7] 更進一步來說，受力必是施加在脛骨和腓骨的上端。但如何建模更符合實際是需要思考的。鑒于此模型要模擬靜止和走路，兩種步態的受力，而模型中卻無一點是限制了自由度的，在分析軟件中一定會得出錯誤的答案。所以，首次嘗試是將腓骨和脛骨各自連接一根桿，向上延伸至同一圓盤，此圓盤的面積大抵為脛骨和腓骨的面積之和，而它的楊氏模量則設為一個極大的值。這樣，他可以被近似為一個剛體，很難有移動。其面積的大小在此情況下也不再重要，設為一個合理值即可。另外，脛骨和腓骨各自連接的桿，其楊氏模量與脛骨或腓骨相同。但這樣一來，施加人自身重力對腳部的壓力的一半，四百五十牛，于每只腳，得到的結果依然呈離散性。經過分析，現有模型，是將膝蓋處設為在水平面上兩方向無自由度，在豎直方向給予限制的自由度，約為0.01mm。但由于膝蓋至脛骨及腓骨的距離較長；即兩桿距離過長，而兩桿本身又無自由度的限制，導入對整個腳部，依然是沒有邊界條件的限制。[8] 因此，最后在脛骨和腓骨自身最上端，沿著同樣的特征形狀向上拓高5mm，建立一個高為5mm的柱體，將三自由度限制和力加在此柱體上。此柱體的楊氏模量設一極大值，數量級大于 。

（二）結合其他軟件進行輸入文件的添加和測試

簡化模型，不單是減少研究人員的分析時間和精力，更是為了完成一整套將來可提供給醫生的體系：醫生在X光片或掃描儀器得到的圖片上點擊所有骨頭上的關鍵幾點，設計的程序可以自動計算出所有點的坐標，由這些軟件自動用接口導入有限元軟件快速建模。[9]

基于此愿景，筆者嘗試了MATLAB、OPENSEES及NASTRAN。[10] 在MATLAB中，主要實現的是生成完全遵循有限元分析軟件輸入文件格式的輸出行。在此過程，簡化的骨頭，由脛骨和腓骨拓展到了所有的骨頭：根據骨頭自身形狀特征的復雜程度，用戶需要輸入的關鍵點數量有所不同；例如脛骨和跟骨需要六個關鍵點，距骨需要九個。通過編寫的程序，可輸出節點的具體坐標。為了了解節點的多少，簡化程度的不同對結果有何影響，可調節兩點間插值點的數量。通過多次嘗試得到的結果與完整腳型的結果進行對比，可以得到一個平衡值，即輸出此數量的簡化模型可以得到與完整腳型最相近的結果，從而實現醫生自己可完成的愿景。為了提前了解輸出行能否在有限元軟件中運行，筆者先用OPENSEES及NASTRAN進行實驗。[11] 同時，在MATLAB中也多添加了畫圖語句，在導入有限元軟件前可以先行查看輸出行中點的坐標是否正確。雖然在整個過程中，不可避免地還是需要利用插值來填補關鍵點之間的空缺，但所需的節點設置遠遠少于八萬個。

（三）仍需優化的細節

對形狀特征復雜的骨頭，仍然需要盡可能多的節點數來精確描繪。但在插值法中，為了要確保所有節點能構成一較光滑曲面，在兩點間需要更精深的數學模型與公式來滿足這一需求。

三、下一步應用

完成有限元腳型的簡化后，對醫生來說，尤其是國外的醫生，向他們推薦全套的自創系統：只需在X光片或掃描儀器得到的圖片上點擊所有骨頭上的關鍵幾點，設計的程序可以自動計算出所有點的坐標，由這些軟件自動用接口導入有限元軟件快速建模。得到結果后，醫生可以針對病人的骨頭形狀及肉質中軟骨筋腱的受損情況，在足弓受力最多、勞損最嚴重的區域放置高度調節裝置，同時也避免了頂住骨頭未能真正分擔受力反增疼痛的情況。對患者，他可以選擇手動調節也可以使用手機程序，來運用調節裝置改變鞋子支持足弓的高度和剛度，從而來滿足患者們對硬度和高度在不同恢復階段的需求。患者們不必再等待整個月并花費巨額的人工費，這對他們確是一個福音。

對研究或產品開發人員來說，對每個腳型也避免了掃描、導入點云進行修改、添加幾萬節點來建模。他們可以遵循和醫生相同的方法更快速地得到受力分布圖。考慮到受力分析結果只是研發的中間步驟，他們或可騰出更多時間精力進行分析和再創作；研究周期也可能會因此縮短。不但如此，對鞋子生產廠家來說，可以批量生產足部恢復鞋。如果在研發過程中，發現對骨頭發育正常或無特異形狀特征的腳型，其受力分布無明顯差異，則對每一個鞋碼，都可以先行確定兩調節裝置的位置。批量生產投入社會就不再是難事。鑒于成品和售價相較起求醫、在不同康復階段來回多次、不斷制作新鞋的費時費錢，好處不言而喻，因而十分具市場潛力。

筆者認為，有限元腳部模型的簡化無論是研發上，還是醫生的實用上，都可起到縮短時間或周期的作用；對病患省時省錢省力，是一大福音的推動器。所有的簡化都建立在人體解剖原理和機械工程的基礎知識，絕無隨意簡化。過程中也參閱了大量文獻來確保任職的正確；借用其他軟件進行輸入文件的添加和測試階段也耗費了大量時間去完善和使結果收斂。

參考文獻：

[1] Riddle， D. L.， Pulisic， M.， Pidcoe， P.， & Johnson， R. E. （2003）. Risk factors for plantar fasciitis： A matched case-control study.Journal of Bone and Joint Surgery，85（5）， 872.

[2] Hornyik， M. L. （2002）.The effects of three months of foot orthotic wear on measures of postural stability in persons with chronic injury and normal lower limb function. [3] Ferede， H. （2011）.A systems approach for point cloud data management.（Order No. 3489446， The George Washington University）.ProQuest Dissertations and Theses， 115-n/a.

[4]馬曉峰.有限元分析從入門到精通[M].北京：清華大學出版社.P22-24

[5] Chen， R. G. （2011）.Finite element analysis of the foot： Metatarsal geometry and indication for stress fractures. ProQuest Dissertations and Theses， 152.

[6] DiDomenico， LA， Fahim， R（Fahim， Ramy）；Rollandini， J（Rollandini， Jobeth） Thomas， ZM（Thomas， Zachary M.）. Correction of Frontal Plane Rotation of sesamoid Apparatus during the Lapidus Procedure： A Novel Approach [J]. JOURNAL OF FOOT & ANKLE SURGERY， MAR-APR 2014（2）： 248-251

[7]Taddei， F.， PhD.， Balestri， M.， M.S.， Rimondi， E.， M.D.， Viceconti， M.， PhD.， & Manfrini， M.， M.D. （2009）. Tibia adaptation after fibula harvesting： An in vivo quantitative study.Clinical Orthopaedics and Related Research，467（8）， 2149-58. doi：http：///10.1007/s11999-009-0776-z

[8] Cheung， M. H. S.， Lee， M.， & Lui， T. H. （2013）. Insufficiency fracture of the proximal fibula and then tibia： A case report.Journal of Orthopaedic Surgery，21（1）， 103-5.

[9] Introduction to finite element analysis using MATLAB and abaqus. （2013）.Reference and Research Book News，28（4）

[10] Dolsek， M. （2010）. Development of computing environment for the seismic performance assessment of reinforced concrete frames by using simplified nonlinear models. Bulletin of Earthquake Engineering，8（6）， 1309-1329.

第5篇：數學建模插值法范文

關鍵詞：主成分分析 內梅羅指數 Muller指數 spss

中圖分類號：O242 文獻標識碼：A 文章編號：1007-3973（2013）007-132-02

1 引言

近些年，人類活動對城市環境影響越來越嚴重。對由人類活動影響造成的城市地質環境的演變模式進行研究，逐漸成為人們關注的焦點。通過文獻[1]提供的某城市城區土壤地質環境進行調查，根據測的的數據，假設樣品采集在充分考慮污染源前提下，兼顧空間分布均勻性，同時考慮地形、氣候因素影響；數據的處理計算時均采用四舍五入法保留小數點后兩位，與原數據保持一致；污染源的重金屬濃度不再增加；取樣點的數據較好的反映了該地區的污染物濃度，對城市表層土壤重金屬的污染進行分析研究。

2 8種主要重金屬元素的空間分布

根據測得數據，采用8種元素在五個地區各自的作用單獨考慮，采用excel軟件繪制標準曲線，對原始數據進行標準化處理，并帶入標準曲線求得各采樣點的重金屬濃度，然后求出平均濃度，再用Muller指數進行各項計算與分析。除此外還采用了地積累指數法和內梅羅綜合指數法進行全面的分析。Muller指數法是對各重金屬元素因子的單獨作用在各地區進行分析，目前國內外普遍采用單因子指數法和內梅羅綜合指數法等進行土壤重金屬污染評價，這兩種方法都能對被研究區域的土壤重金屬污染程度進行較為全面的評價，但不能從自然異常中分離人為異常，判斷表生過程中重金屬元素的人為污染情況，但地累積指數法彌補了其他評價方法的不足。

2.1 重金屬元素在該城區的空間分布圖

用雙調和樣條內行插值計算，得出重金屬空間分布圖。雙調和技術在二維或多維空格鍵中的導數與一維空間中的導數的作用相似。在m維空間中，利用N個數據點的曲面求解問題：；其中，是雙調和算子，x是m維空間中的一個位置。其通解為，求解線性系統，可以得到。

在EXCEL中分別篩選出每一區的8種重金屬濃度情況，由于給出的重金屬量綱不統一，用歸一化方法統一量綱。然后分別在每一區內對不同重金屬求平均值主要重金屬元素關于該城市五個區的分布。

Sij表示規劃后某種金屬濃度在某個采樣點的值，xij某種重金屬在某個采樣點的值。由歸一化后，運用富集系數模型：Di=d實測值 / b背景值定量描述城市重金屬污染的空間分布情況。

2.2 三種評價不同區域重金屬的污染程度的方法

2.2.1 地積累指數法

國內外很多專家將地積累指數法用于對人類活動造成的重金屬對土壤污染的評價。該指數的計算式為：Igeo=log2[Cn/（kBn）]。根據Igeo值將污染等級分為6級，并且以國家二級標準作基準的污染評價。

2.2.2 內梅羅綜合指數分析法

內梅羅指數法是當前國內外進行綜合污染指數計算的最常用的方法之一。該方法先求出各因子的分指數（超標倍數），然后求出各分指數的平均值，取最大分指數和平均值計算。綜合污染指數計算公式：。內梅羅綜合指數在評價時可能會人為地夸大或縮小一些因子的影響作用，使其對環境質量評價的靈敏性不夠高，有時候計算結果很難區分土壤環境污染程度的差別。所以，采用污染負荷指數法數學模型進行進一步分析。

2.2.3污染負荷指數法

用污染負荷指數法以土壤背景值為評價標準，對整個區域各個點位各種重金屬進行定量分析，并對各點的污染程度進行分級，反映對環境污染最嚴重的元素。

3 分析重金屬污染物的傳播特征

為了分析研究各種土壤重金屬的來源，本文采用了Pearson相關分析對被研究區域8中重金屬含量數據進行了相關分析。從相關性分析結果可以發現，土壤中Pb與Cd，Ni與As顯著正相關，且相關性較強，分別為0.812、0.639；其次為Cu與Cd，Cr與Ni，Pb和Cu也達到正相關。

本文對所有采樣點采取主成分分析法，利用SPSS 13.0軟件對城區土壤重金屬的5項指標進行主成分分析。通過主成分分析計算，城區的8個變量的全部信息可由5個主成分表示，即對前5個主成分進行分析已經能夠反映全部數據的大部分信息，再由5個主成分加權平均得出每個采樣點相對應的綜合指標。

基于SPSS軟件包軟件包生成的因子成分得分系數矩陣，降維后每種成分在每個取樣點的得分計算公式：

綜合指標的得分計算公式：

根據問題一中的方法參考Zj對應的取樣點坐標對Zj做插值處理，并繪制等高線圖，可得圖1。

圖1 等高線圖

由圖1可以看出，在靠近坐標原點的地方有兩個綜合指數超高區，可以認為這兩個區域既是污染源所在的區域。

通過使用MATLAB進行雙調和樣條插值法，由Zj生成了一個200*200的矩陣。可以通過程序將其轉換成一個具有200*200個元素的矩陣。可以得出綜合指數Z的分布主要集中在0到0.2的區間中。我們認為污染源受到污染的水平應當遠高于距離污染源較遠的地方。所以我們將主要通過研究Z大于0.2的點來確認污染源。經過excel的篩選，大于0.2的點有1805個。污染源必然包含在這些點中間。

結合重金屬在土壤中的傳播特征，建立數學模型

4 結論

為更好地研究城市地質環境的演變模式，預測土壤中各種重金屬的含量，必須求解并分析城市內土壤中各種重金屬污染物的主要來源，確定影響這些重金屬含量時間變化的主要影響因子并進行分析，然后在分析的結果中建立各種土壤重金屬含量的時間預測模型。得重金屬累積預測模型如下：

通過建立的模型可以用以城市土壤環境異常分析，以及城市環境質量評價，測定各區域重金屬含量等，具有較強的實際應用價值。

參考文獻：

第6篇：數學建模插值法范文

【關鍵詞】半參數模型 完善誤差 測量值 縱向數據

本文以半參數模型為例，對參數、非參數分量的估計值和觀測值等內容進行討論，并運用三次樣條函數插值法得出非參數分量的推估表達式。另外，為了解決縱向數據下半參數模型的參數部分和非參數部分的估計問題，在誤差為鞅差序列情形下，對半參數數據模型、漸近正態性、強相合性進行研究和分析。另外，本文初步討論了平衡參數的選取問題，并充分說明了泛最小二乘估計方法以及相關結論，同時對半參數模型的迭代法進行了相關討論和研究。

一、概論

在日常生活當中，人們所采用的參數數據模型構造相對簡單，所以操作起來比較容易；但在測量數據的實際使用過程中存在著相關大的誤差，例如在測量相對微小的物體，或者是對動態物體進行測量時。而建立半參數數據模型可以很好的解決和緩解這一問題：它不但能夠消除或是降低測量中出現的誤差，同時也不會將無法實現參數化的系統誤差進行勾和。系統誤差非常影響觀測值的各種信息，如果能改善，就能使其實現更快、更及時、更準確的誤差識別和提取過程；這樣不僅可以提高參數估計的精確度，也對相關科學研究進行了有效補充。舉例來說，在模擬算例及坐標變換GPS定位重力測量等實際應用方面，體現了這種模型具有一定成功性及實用性；這主要是因為半參數數據模型同當前所使用的數據模型存在著一致性，可以很好的滿足現在的實際需要。而新建立的半參數模型以及它的參數部分和非參數部分的估計，也可以解決一些污染數據的估計問題。這種半參數模型，不僅研究了縱向數據下其自身的t型估計，同時對一些含光滑項的半參數數據模型進行了詳細的闡述。另外，基于對稱和不對稱這兩種情況，可以在一個線性約束條件下對參數估計以及假設進行檢驗，這主要是因為對觀測值產生影響的因素除了包含這個線性關系以外，還受到某種特定因素的干擾，所以不能將其歸入誤差行列。另外，基于自變量測量存在一定誤差，經常會導致在計算過程匯總，丟失很多重要信息。

二、半參數回歸模型及其估計方法

這種模型是由西方著名學者Stone在上世紀70年代所提出的，在80年代逐漸發展并成熟起來。目前，這種參數模型已經在醫學以及生物學還有經濟學等諸多領域中廣泛使用開來。

半參數回歸模型介于非參數回歸模型和參數回歸模型之間，其內容不僅囊括了線性部分，同時包含一些非參數部分，應該說這種模型成功的將兩者的優點結合在一起。這種模型所涉及到的參數部分，主要是函數關系，也就是我們常說的對變量所呈現出來的大勢走向進行有效把握和解釋；而非參數部分則主要是值函數關系中不明確的那一部分，換句話就是對變量進行局部調整。因此，該模型能夠很好的利用數據中所呈現出來的信息，這一點是參數回歸模型還有非參數歸回模型所無法比擬的優勢，所以說半參數模型往往擁有更強、更準確的解釋能力。

從其用途上來說，這種回歸模型是當前經常使用的一種統計模型。其形式為：

三、縱向數據、線性函數和光滑性函數的作用

縱向數據其優點就是可以提供許多條件，從而引起人們的高度重視。當前縱向數據例子也非常多。但從其本質上講，縱向數據其實是指對同一個個體，在不同時間以及不同地點之上，在重復觀察之下所得到一種序列數據。但由于個體間都存在著一定的差別，從而導致在對縱向數據進行求方差時會出現一定偏差。在對縱向數據進行觀察時，其觀察值是相對獨立的，因此其特點就是可以能夠將截然不同兩種數據和時間序列有效的結合在一起。即可以分析出來在個體上隨著時間變化而發生的趨勢，同時又能看出總體的變化形勢。在當前很多縱向數據的研究中，不僅保留了其優點，并在此基礎之上進行發展，實現了縱向數據中的局部線性擬合。這主要是人們希望可以建立輸出變量和協變量以及時間效應的關系。可由于時間效應相對比較復雜，所以很難進行參數化的建模。

另外，雖然線性模型的估計已經取得大量的成果，但半參數模型估計至今為止還是空白頁。線性模型的估計不僅僅是為了解決秩虧或病態的問題，還能在百病態的矩陣時，提供了處理線性、非線性及半參數模型等方法。首先，對觀測條件較為接近的兩個觀測數據作為對照，可以削弱非參數的影響。從而將半參數模型變成線性模型，然后，按線性模型處理，得到參數的估計。而多數的情況下其線性系數將隨著另一個變量而變化，但是這種線性系數隨著時間的變化而變化，根本求不出在同一個模型中，所有時間段上的樣本，亦很難使用一個或幾個實函數來進行相關描述。在對測量數據處理時，如果將它看作為隨機變量，往往只能達到估計的作用，要想在經典的線性模型中引入另一個變量的非線性函數，即模型中含有本質的非線性部分，就必須使用半參數線性模型。另外就是指由各個部分組成的形態，研究對象是非線性系統中產生的不光滑和不可微的幾何形體，對應的定量參數是維數，分形上統計模型的研究是當前國際非線性研究的重大前沿課題之一。因此，第一種途徑是將非參數分量參數化的估計方法，也稱之為參數化估計法，是關于半參數模型的早期工作，就是對函數空間附施加一定的限制，主要指光滑性。一些研究者認為半參數模型中的非參數分量也是非線性的，而且在大多數情形下所表現出來的往往是不光滑和不可微的。所以同樣的數據，同樣的檢驗方法，也可以使用立方光滑樣條函數來研究半參數模型。

四、線性模型的泛最小二乘法與最小二乘法的抗差

（一）最小二乘法出現于18世紀末期

在當時科學研究中常常提出這樣的問題：怎樣從多個未知參數觀測值集合中求出參數的最佳估值。盡管當時對于整體誤差的范數，泛最小二乘法不如最小二乘法，但是當時使用最多的還是最小二乘法，其目的也就是為了估計參數。最小二乘法，在經過一段時間的研究和應用之后，逐步發展成為一整套比較完善的理論體系。現階段不僅可以清楚地知道數據所服從的模型，同時在縱向數據半參數建模中，輔助以迭代加權法。這對補償最小二乘法對非參數分量估計是非常有效，而且只要觀測值很精確，那么該法對非參數分量估計更為可靠。例如在物理大地測量時，很早就使用用最小二乘配置法，并得到重力異常最佳估計值。不過在使用補償最小二乘法來研究重力異常時，我們還應在兼顧著整體誤差比較小的同時，考慮參數估計量的真實性。并在比較了迭代加權偏樣條的基礎上，研究最小二乘法在當前使用過程中存在的一些不足。應該說，該方法只強調了整體誤差要實現最小，而忽略了對參數分量估計時出現的誤差。所以在實際操作過程中，需要特別注意。

（二）半參模型在GPS定位中的應用和差分

半參模型在GPS相位觀測中，其系統誤差是影響高精度定位的主要因素，由于在解算之前模型存在一定誤差，所以需及時觀測誤差中的粗差。GPS使用中，通過廣播衛星來計算目標點在實際地理坐標系中具體坐標。這樣就可以在操作過程中，發現并恢復整周未知數，由于觀測值在衛星和觀測站之間，是通過求雙差來削弱或者是減少對衛星和接收機等系統誤差的影響，因此難于用參數表達。但是在平差計算中，差分法雖然可以將觀測方程的數目明顯減少，但由于種種原因，依然無法取得令人滿意的結果。但是如果選擇使用半參數模型中的參數來表達系統誤差，則能得到較好的效果。這主要是因為半參數模型是一種廣義的線性回歸模型，對于有著光滑項的半參數模型，在既定附加的條件之下，能夠提供一個線性函數的估計方法，從而將測值中的粗差消除掉。另外這種方法除了在GPS測量中使用之外，還可應用于光波測距儀以及變形監測等一些參數模型當中。在重力測量中的應用在很多情形下，尤其是數學界的理論研究，我們總是假定S是隨機變量實際上，這種假設是合理的，近幾年，我們對這種線性模型的研究取得了一些不錯的成果，而且因其形式相對簡潔，又有較高適用性，所以這種模型在諸多領域中發揮著重要作用。

通過模擬的算例及坐標變換GPS定位重力測量等實際應用，說明了該法的成功性及實用性，從理論上說明了流行的自然樣條估計方法，其實質是補償最小二乘方法的特例，在今后將會有廣闊的發展空間。另外文章中提到的分形理論的研究對象應是非線性系統中產生的不光滑和不可微的幾何形體，而且分形已經在斷裂力學、地震學等中有著廣泛的應用，因此應被推廣使用到研究半參數模型中來，不僅能夠更及時，更加準確的進行誤差的識別和提取，同時可以提高參數估計的精確度，是對當前半參數模型研究的有力補充。

五、總結

文章所講的半參數模型包括了參數、非參數分量的估計值和觀測值等內容，并且用了三次樣條函數插值法得到了非參數分量的推估表達式。另外，為了解決縱向數據前提下，半參數模型的參數部分和非參數部分的估計問題，在誤差為鞅差序列情形下，對半參數數據模型、漸近正態性、強相合性進行研究和分析。同時介紹了最小二乘估計法。另外初步討論了平衡參數的選取問題，還充分說明了泛最小二乘估計方法以及有關結論。在對半參數模型的迭代法進行了相關討論和研究的基礎之上，為迭代法提供了詳細的理論說明，為實際應用提供了理論依據。

參考文獻

[1]胡宏昌.誤差為AR（1）情形的半參數回歸模型擬極大似然估計的存在性[J].湖北師范學院學報（自然科學版），2009（03）.

[2]錢偉民，李靜茹.縱向污染數據半參數回歸模型中的強相合估計[J].同濟大學學報（自然科學版），2009（08）.

[3]樊明智，王芬玲，郭輝.縱向數據半參數回歸模型的最小二乘局部線性估計[J].數理統計與管理，2009（02）.

[4]崔恒建，王強.變系數結構關系EV模型的參數估計[J].北京師范大學學報（自然科學版）.2005（06）.

[5]錢偉民，柴根象.縱向數據混合效應模型的統計分析[J].數學年刊A輯（中文版）.2009（04）

[6]孫孝前，尤進紅.縱向數據半參數建模中的迭代加權偏樣條最小二乘估計[J].中國科學（A輯：數學），2009（05）.

[7]張三國，陳希孺.EV多項式模型的估計[J].中國科學（A輯），2009（10）.

[8]任哲，陳明華.污染數據回歸分析中參數的最小一乘估計[J].應用概率統計，2009（03）.

[9]張三國，陳希孺.有重復觀測時EV模型修正極大似然估計的相合性[J].中國科學（A輯）.2009（06）.

[10]崔恒建，李勇，秦懷振.非線性半參數EV四歸模型的估計理論[J].科學通報，2009（23）.

[11]羅中明.響應變量隨機缺失下變系數模型的統計推斷[D].中南大學，2011.

[12]劉超男.兩參數指數威布爾分布的參數Bayes估計及可靠性分析[D].中南大學，2008.

[13]郭艷.湖南省稅收收入預測模型及其實證檢驗與經濟分析[D].中南大學，2009.

[14]桑紅芳.幾類分布的參數估計的損失函數和風險函數的Bayes推斷[D].中南大學，2009.

第7篇：數學建模插值法范文

關鍵詞：計算方法；教學改革；應用型人才；人才培養模式；創新能力

計算方法課程是高等院校本科層次信息與計算專業的核心課程，其教學目標是使學生掌握數值計算和程序設計方法，提高科學計算中分析和解決實際問題的能力。隨著社會的進步和計算機技術的快速發展，數值計算方法已經廣泛應用到生物、經濟、材料、制造、氣象、設計等諸多領域，使得學生掌握這一專業知識顯得尤為重要[1]。盡管經過幾十年的建設和發展，計算方法研究的理論體系逐步完善，教材和相關教輔著作日趨豐富，但是該課程的教學仍然存在教學觀念陳舊、教學方法落后和重理論輕實踐的問題，不能滿足新形勢下應用型人才培養目標的要求[2]。鑒于此，本文就當前計算方法課程存在的問題，結合本人從事該課程教學積累的經驗，從教學觀念、教學內容和教學模式等方面探討該課程的教學改革思路。

一、計算方法課程的特點及教學中存在的不足

(一)計算方法課程的特點

計算方法課程的內容較多，涉及高等數學、線性代數、微分方程、泛函分析等方面的知識，且其理論性較強，尤其是算法推導、穩定性分析、收斂性分析、誤差分析等內容。計算方法課程各章節知識之間的獨立性強，連貫性弱，且數學公式繁多、復雜、抽象，不利于學生記憶[1]。計算方法是一個將數學科學和計算機科學結合在一起的交叉學科，同一數值計算問題的解決可以有許多不同的方法，不同算法的計算誤差和計算效率也不相同，而問題的解決最終要通過編寫計算機程序來實現，具有較強的實踐性。

(二)計算方法課程教學中存在的不足

根據筆者的教學經驗和體會，目前該課程教學中主要存在如下幾個方面的問題：1.既有教材難以很好地滿足教學要求近年來，筆者所在的計算方法課程教學組先后選用了不同版本的教材，但感覺到這些教材都不能很好地滿足應用型創新人才培養的需要。例如，李慶揚主編的《數值分析》是很多本科院校理工科使用的一部經典的優秀教材，其理論性強，內容豐富，但在應用方面有所欠缺，不能很好地滿足應用型人才培養的需要。再如，王能超編寫的《數學分析簡明教材》具有內容精煉、深入淺出、通俗易懂的特點，是高等院校一般工科專業計算方法課程的優秀教材，但由于該教材較少涉及算法實際的應用背景，且對算法實現內容的介紹較少，因此易導致學生學習興趣不高，不能很好地滿足應用型本科院校教學的需要。2.實踐教學內容匱乏在不少高校，計算方法課程計劃中安排的學時•152•數普遍較少，如筆者授課的班級，該課程總共安排48學時，其中理論課32學時，上機實驗課16學時。由于學時的限制，使得課程教學內容多為以公式推導為主的理論知識，上機實驗僅限于驗證教材上的一些基本算法，極少將數學建模思想融入實驗教學中。這種缺乏應用性和趣味性的實驗教學，難以激發學生的興趣，更難以有效提高學生解決實際問題的能力。3.教學手段和方式單一板書是一種重要的教學手段，但對于復雜的理論分析和公式推導，單一的板書式教學不利于吸引學生的注意力和興趣。將板書式教學與多媒體教學有機結合起來，可以有效提高課堂教學質量，但在計算方法課程教學中，有的教師單調地進行板書式教學而排斥多媒體教學，有的教師則過度依賴多媒體教學手段而放棄板書式教學，從而影響了教學效果。在教學方式方法上，由于教學內容多而學時有限，一些教師在授課時一味地采用講授式教學法，極少開展討論式教學和任務驅動式教學，致使課堂氣氛嚴肅有余而活躍不足，學生學習的主動性和積極性沒有得到充分發揮。4.課程考核方式單一在很多高校，計算方法課程的考核方式和其他理論課幾乎完全相同，即僅重視結論性考核而輕視過程性考核，且結論性考核多以閉卷考試的方式進行，對實踐環節的考核不足。該課程考核方式的導向作用決定了學生在學習的過程中重理論而輕實踐，進而造成了學生算法設計水平不高和解決實際問題的能力不強的狀況[4]。

二、計算方法課程改革的思路

(一)更新教學觀念

要改變計算方法課程教學效果不佳、學生解決實際問題能力不強的局面，教師必須更新教學觀念，打破以往重理論輕實踐的教學觀念和教學模式。作為教學活動的組織者和引導者，教師不但要準確、高效地傳授課本知識，而且要指導學生學會學習和應用，讓學生從被動聽講的知識接受者轉變為主動學習的知識探究者，只有這樣才能充分調動學生學習的主動性和積極性。因此，從事計算方法課程教學的教師，必須以“厚基礎、重能力、強創新”的人才培養目標為指引，將學生素質的提高和創新能力的培養置于課程教學的中心地位，采用靈活多變的教學方式和方法來調動學生的學習興趣，強化和培養學生運用所學知識解決實際問題的能力[5]。

(二)優化教學內容

1.優化理論教學內容計算方法課程主要包含插值法、數據擬合、數值積分、微分方程數值解法、方程求根、線性方程組的迭代法和直接法等內容。該課程學時較少，涉及知識面較寬，抽象性較強，并且涉及繁雜的算法、公式推導和理論分析，對學習者計算機編程能力的要求也較高，為了確保學生能在有限的學時內有效地掌握算法的設計思想、程序流程、誤差的估計和分析方法，培養提高學生以計算機為工具、運用數值計算方法解決實際問題的能力，教師必須在新教學理念的指導下優化課程內容。為了適應應用創新型人才培養的要求，計算方法課程宜選用理論和實踐并重、實用性強、案例豐富的教材。在缺乏理想教材的情況下，教師應根據教學需要靈活整合教學內容，力求對知識點的講解做到詳略得當，比如，對于理論證明可稍微簡略一些，而對于算法思想、算法設計和算法的應用應詳細講解。2.強化實驗教學以往計算方法課程的實踐教學僅僅要求學生實現教材上一些基本的算法，實驗內容缺乏精心設計，很難適應新形勢下應用型人才培養的要求。因此，必須對以往的實驗內容進行整合和優化，除了對教材提供的基本算法進行驗證以外，還需要增加一些兼具趣味性和實用性的綜合實驗內容。比如，在數值積分部分，可以讓學生進行空中電纜長度計算的實驗；在數據擬合部分，可以讓學生進行給藥方案設計的實驗；在微分方程數值解部分，可以讓學生利用微分方程數值計算方法和已知觀測數據進行模型參數估計實驗。為了滿足不同層次學生的要求，實驗可以分為必做和選做兩種。對于選做性實驗（如一些數學建模試驗），可以讓學生以自由組隊的方式來進行，這樣不但能達到完成既定教學目標的目的，還能強化提高學生的團隊合作能力和創新能力。優化實驗教學內容，應著力于使學生靈活地應用和創造性地改進教材提供的一些標準數值算法，以實現培養應用型創新人才的目標。

(三)改革教學方法、教學手段與課程考核方式

計算方法是一個“數學思維和數值思想、學數學和用數學、理論與實踐相結合的交叉學科”。因此，單一地采用傳統的講授式教學法很難實現計算方法課程的教學目標，只有進行教學方式和教學手段的改革，才能有效地提高教學效果。1.教學方式的改革在計算方法課程教學中，教師宜采用靈活多樣的研討式、辯論式和啟發式教學，注重課堂交流互動，充分激發學生的學習興趣，調動學生參與課堂活動的積極性。對算法的講解應注重講解算法的設計思想、算法的流程、算法的誤差、不同算法間的比較和計算復雜度的分析，并摒棄滿堂灌的廣播式教學，給學生留下獨立思考的時間；應結合當前學術研究的前沿問題，對課本知識進行適當的擴充，以開拓學生的視野，拓展學生的思維空間，提高學生學習的興趣和主動性。例如，在講解微分方程數值解的過程中，除了介紹歐拉方法、改進的歐拉方法及龍格庫塔方法的設計思想、誤差估計和計算的復雜度討論以外，可以引導學生運用所學知識來探討系數是分段函數和周期函數的常微分方程、脈沖微分方程、泛函微分方程、隨機微分方程的數值解等問題的解決方案，然后通過課堂交流討論不斷優化算法，最終完成計算機編程并進行課堂演示。這種教學方式有利于培養學生的創新能力。2.教學手段的改革計算方法課程的理論性和實踐性決定了僅采用傳統的“一根粉筆走天下”的單一教學手段不能滿足應用型人才培養的需要。多媒體教學具有直觀性、高效性、交互性、集成性等特點，將課程中抽象、枯燥的學習內容通過圖形、動畫等形式直觀地呈現給學生，有利于提高教學效率，增強教學效果。因此，在計算方法課程的教學中，教師應將多媒體教學和傳統的“黑板+粉筆”板書教學結合起來，如概念介紹、圖形演示、應用軟件和程序設計分析等內容采用多媒體教學方式，而定理的證明則采用板書式教學。

(四)課程考核方式的改革

通過計算方法課程的教學，既要讓學生掌握算法設計思想和誤差分析的理論知識，又要讓學生掌握算法設計和上機調試的基本技能，最終能熟練運用Matlab編制具體算法去解決實際問題。計算方法課程的教學目標決定了其考核方式不能像其他數學課程一樣僅僅依據理論知識考試成績衡量學生的學習效果。單一的理論考核不利于調動學生進行程序設計和上機實驗的積極性，也不能全面考查學生對該課程的掌握情況。該課程較為合理的考核方式應該采用專題論文、理論試卷與上機編程相結合的方式。各種方式考核的權重，以平時考勤和作業成績占10%、上機編程占25%、專題論文占15%和期末考試占50%較為合適[6]。隨著應用型本科高校轉型發展工作的推進，計算方法課程的教學改革已經勢在必行。本文結合計算方法課程在教學上存在的一些普遍問題，結合應用型創新人才培養的要求，從更新教學觀念、優化教學內容、改進教學方法和完善考核方式等方面對該課程的教學改革進行了初步的探討與研究。教學實踐表明，這些措施有利于提高教學效果，尤其在激發學生的創新思維意識、提高學生運用所學理論解決實際問題的能力方面成效顯著。

參考文獻：

[1]張俊麗．“數值計算方法”課程的教學改革探索[J]．中國電力教育，2012(10)：87―88．

[2]王金柱．計算方法課程教學改革的探索與實踐[J]．陜西教育學院學報，2011(1)：81―83．

[3]王曉峰．計算方法課程教學改革探討[J]．呂梁教育學院學報，2009(3)：64―66．

[4]李華，邵維，楊雪松，等．《數值計算方法》課程教學改革實踐與探討[J]．實驗科學與技術，2013(5)：256―258．

[5]徐建敏，熊金志，李勇．地方高校“計算方法”實驗教學的改革[J]．實驗室研究與探索，2011(9)：152―154．

第8篇：數學建模插值法范文

【關鍵詞】折疊紙盒 有限元法 強度 等效模擬

折疊紙盒憑借其原材料的環保性、可裝潢性、可印刷性等其他包裝不可替代的特性[1]，在物資流通和包裝行業深受人們的青睞，廣泛應用于食品、藥品、化妝品、煙酒等日常生活用品的包裝。盡管折疊紙盒不是運輸包裝容器，但作為一種“剛”性包裝容器而言，折疊紙盒也應具有足夠的強度來抵抗變形和破壞的力量，才能對商品提供足夠的保護和便于銷售時對商品進行陳列和展示[2]。

近年來，國內外學者對折疊紙盒的抗壓強度進行了不少研究，王金林[3]論證了紙盒抗壓強度和白板紙挺度的關系；Grangard[4]通過大量的試驗確定經驗公式BRDA式具有較高的相關性；余本農[2]根據瓦楞紙箱抗壓強度公式推導出折疊紙盒的經驗公式；劉慧和張新昌[5-6]研究了管式折疊紙盒的結構和幾何尺寸對抗壓強度的影響，并且探討折疊紙盒抗壓強度經驗計算公式；袁毅等[7]研究鎖底結構形式對紙盒承載力的影響。但以上學者的研究主要還停留在試驗研究的基礎上，由于試驗的不穩定性以及各種尺寸折疊紙盒試驗樣品獲取困難，要想更好地掌握折疊紙盒承載能力和抗壓變形能力不能只停留在單純的試驗研究上，應該從原材料自身入手，結合理論與試驗結論，借助于有限元分析技術來對折疊紙盒承載能力和抗壓變形能力進行仿真模擬，不僅可以縮短實驗周期，節約試驗費用，還能夠對紙盒各個部位作研究和討論，更為直觀地得到折疊紙盒各個部位的力學狀態對包裝性能的影響。

1 有限元法的概念

有限單元法最初是20世紀50年代作為處理固體力學問題的方法出現的，并隨著電子計算機的發展而迅速發展起來的一種現代計算方法。作為計算機輔助工程CAE的一種，使用它大大提高了產品開發、設計、分析和制造的效率和產品性能[8]。

有限元法是一種基于變分法而發展起來的求解微分方程的數值計算方法，其基本思想是把一個連續的介質（或構件）看成是由有限數目的單元組成的集合體，并在每一個單元中設定有限數量的節點，在各單元內假定具有一定的理想化的位移和應力分布模式，各單元間通過節點相連接，并藉以實現應力的傳遞，各單元之間的交接面要求位移協調，利用彈性力學、固體力學、結構力學等力學中的變分原理去建立一套線性方程組，從而將一個連續域中的無限自由度問題轉化為離散域中的有限自由度問題，求解這些方程組，便可得到各單元和結點的位移、應力。簡言之，就是用較簡單的問題代替復雜問題后再求解，即化整為零分析，積零為整研究。對于不同物理性質和數學模型的問題，有限元求解法的基本步驟是相同的，分為前處理、處理和后處理3個階段，只是具體公式推導和運算求解不同。

2 有限元法在分析紙盒強度時要考慮的問題

2.1 研究參數的選取問題

根據理論分析可以得出，折疊紙盒的抗壓強度受到紙板原材料性能以及紙盒的結構形式和結構參數的影響。紙板原材料性能包括紙板的環壓強度、挺度、厚度和定量等，紙盒結構形式包括管式、盤式、管盤式和非管非盤式等，紙盒結構參數主要指的是紙盒的幾何尺寸長、寬和高。對于研究紙盒強度問題，在單純的試驗研究時首先是確定紙板原材料和紙盒結構形式，然后對改變不同幾何結構參數的紙盒進行測試，看紙盒是否滿足強度和剛度的要求。

其實，紙盒的結構形式和原材料性能在很大程度上決定了紙盒的特點和工藝效果，提高紙板的挺度和環壓強度，優化紙盒的結構和幾何尺寸都可以提高紙盒的抗壓強度，若是僅僅靠改變結構參數來研究紙盒強度性能，很難做到對紙盒抗壓強度的系統化研究。而且目前對紙盒強度的研究主要是基于“設計―盒樣―試驗―修改”不斷循環的優化過程模式，這樣既麻煩又浪費大量成本。所以在基于有限元法研究紙盒各個參數的同時還應該考慮紙盒結構形式、原材料屬性以及還未進行過研究的參數。另外，有限元模擬分析既可以針對某一參數變量的研究，也可以對多參數的交互作用進行研究，我們可以根據需要靈活運用。

2.2 有限元等效模擬分析問題

有限元法對紙盒壓縮過程的數值模擬就是利用一定的方法，將結構和應力變化的復雜過程近似模擬出來，它包括結構靜力學的計算和結構非線性的計算兩部分。在有限元仿真模擬分析中，幾何實體模型的建立及簡化、單元類型的選取、有限元網格模型的生成、約束條件的設置和載荷的施加都顯得尤為重要，它們都將直接影響到最終仿真計算結果的精確性。

（1）幾何模型建立及簡化問題

折疊紙盒的受力壓縮過程是一個實際問題，考慮到壓縮的復雜性和多樣性對有限元分析計算結果的影響，必須對紙盒結構進行合理簡化，把實際結構簡化成計算模型，然后再利用有限元法來分析解決問題。為了方便有限元建模及計算，在不失真的前提下，對紙盒結構可做如下的簡化處理。

①鑒于紙板原材料的特性，將紙板等效成一塊正交各向異性的復合材料板；②忽略非承載件的影響，將紙盒的六個面板都看作是四邊簡支板，忽略紙盒上的小結構，如側板上的襟片以及插舌等；③認為結構中的粘合是理想粘合，忽略襟片粘合不牢所引起的強度弱化問題。

由于紙盒結構規則，對紙盒結構進行合理簡化之后，可以選擇直接在有限元分析軟件ANSYS中采用“自底向上”法建立模型。需要注意的是，簡化一些無關緊要的細節能使分析求解盡可能地高效，但是隨著襟片和其它一些細節被簡化，在它們鄰近區域內仿真模擬計算出的應力值可能不準確，導致該區域計算的結果不能反映真實應力。因此，可以考慮采用在模型中添加該細節重新計算、子模型法和外插值法3種方案對局部應力進行考察。

（2）單元類型選擇問題

在有限元分析過程中，對于不同的問題，需要應用到不同特性的單元，ANSYS單元庫中提供了超過250種的不同單元類型，每一種單元都是專門為有限元問題而設計的。因此，單元選擇不當，直接影響到計算能否進行和計算結果的精度。根據紙板原材料的結構，由于紙板的厚度相對較薄，理論上可以將其簡化為正交各向異性薄板。在薄板構件的有限元分析中，一般采用殼體單元或者三維實體單元進行分析。根據國內外一些研究資料和有限元分析數據，采用殼體單元對紙板結構進行分析可以獲得足夠精確的結果，并且采用殼體單元分析可以比采用實體單元分析節省大量的時間。

殼單元是為有效建立薄的結構而特別設計的單元類型，它用于主尺寸不小于10倍厚度的結構。ANSYS中提供了一系列殼體單元，常見的有：SHELL63、SHELL43、SHELL93、SHELL181等。其中SHELL181是一個4節點的四邊形薄板殼結構，如圖1所示，它含有I、J、K、L四個節點，每個節點含有6個自由度，即沿X、Y、Z方向上的三個平動自由度和繞X、Y、Z軸的三個轉動自由度。它可以支持材料塑性、應力剛化、大應變，適用于從薄到中等厚度的薄板殼結構。因此，根據紙板本身特性和紙盒壓縮的實際過程，為了獲得更精確的模擬數據，建議選擇SHELL181單元類型進行分析。

（3）網格劃分問題

ANSYS的運算最終是通過有限單元法進行，因此對建立好的幾何模型進行網格劃分是ANSYS分析的一個重要內容。網格劃分直接影響到計算結果的精度和計算速度，甚至會因為網格劃分不合理而導致計算不收斂。目前對于網格劃分，有兩種劃分方式：自由網格劃分和映射網格劃分，這兩種網格劃分方法各有優缺點。自由網格劃分適合于初學者使用，劃分耗時較少，而映射網格計算結果的精度一般要高于自由網格的計算精度。充分考慮到紙盒各部位的結構，可以采用自由網格劃分和映射網格劃分相結合的方法。對紙盒面板結構使用自由網格劃分，在可能出現應力集中的位置或擬定的重點考察位置采用映射網格劃分，使之能以較高的精度得到這些位置的應力，從而保證計算結果的精度。

另外，網格數量的多少影響計算結果的精度和計算分析時間，但并非網格劃分的越細得到的結果就越好，因為網格太密太細，會占用大量的分析時間。為了考察網格劃分的合理程度，在計算模型建立后進行試算，以考察模型精度，特別是重點考察區域的精度。對于紙板類結構，保證單元邊長在lmm-2mm之間時基本都能取得理想的結果。

（4）約束與加載問題

建立紙盒有限元分析模型應當在每個坐標軸方向上至少給定一個約束，受約束節點的數量根據實際情況具體確定。定義約束條件是一個容易產生較大誤差的地方，紙盒的約束是根據其具體結構確定的。紙盒的壓縮試驗是在上下兩塊光滑的壓盤上進行的，顯然壓盤的剛度比紙盒大的多，上壓盤以緩慢的速度加載，最后將紙盒壓潰。當紙盒在水平壓盤上加載受壓時由于摩擦力的作用與上壓盤接觸的紙盒面板只會沿豎直方向被壓縮，而與下壓盤接觸的紙盒面板相當于被固定在水平的壓盤上，不會有水平的滑動也沒豎直方向的壓縮。故對紙盒施加約束時，應將紙盒受壓時的邊界約束條件等效化，根據紙盒的受力以及實際破壞情況，紙盒面板與上下壓盤接觸的各節點豎向位移耦合，與上壓盤接觸的各節點豎向位移耦合，施加共同向下的位移，下壓盤固定不動，對與下壓盤接觸的各節點的所有自由度施加約束，即對紙盒模型的四個側板的底部進行約束，保證這些部位的節點不發生平動或轉動。

在ANSYS分析中，載荷包括邊界條件和內外部的作用力函數，在不同的分析領域中具有不同的表征，為了真實地反映實際物理情況，將載荷分為自由度約束（DOF）、集中力載荷、面載荷、體載荷、慣性載荷以及耦合場載荷等。載荷可以直接在實體模型上加載，如將載荷施加到關鍵點、線或者面上；也可以在有限元模型上加載，即直接將載荷施加到節點和單元上。這兩種方法各有利弊，但無論選用何種途徑加載，程序都會自動將這些載荷轉移到有限元模型上。在紙盒壓縮過程中，紙盒面板主要承受壓盤施加的作用力，為了模擬實際壓縮情況，應該選擇在紙盒上加一個剛體，最后在剛體上施加一定載荷。

（5）非線性求解問題

紙盒的受力壓縮過程是一個囊括了材料、狀態、幾何三種非線性問題的復雜受力過程。材料非線性是指紙板原材料的應力-應變關系引起的非線，而且是不可逆轉的；狀態非線性是指紙板壓縮后引起的接觸問題；幾何非線性是指紙板在壓縮的過程中其變化的幾何形狀引起的非線性響應，屬于大應變類型。作為復雜的非線性分析，涉及到求解器的選擇、載荷步長的選取、子步數的設置、迭代收斂準則、自動時間步長等許多非線性因素，求解設置比較復雜，若處理不當就會造成分析結果不收斂或者分析中斷等情況出現。因此，為了保證模擬計算的順利實現并獲得準確的計算結果，在前期求解設置時可以針對不同情況進行多次試算，以獲取最佳的求解設置參數，特別是控制好平衡迭代及收斂準則之間的關系。

結語

近年來，隨著計算機技術、現代力學和計算數學的發展，有限元法作為一個具有堅實理論基礎和廣泛應用效力的數值模擬分析工具，在包裝工程領域方面的應用越來越多。包裝設計及研究人員將這種技術引入到研究包裝材料的系統中，不僅提供了一種新的研究思路，而且有效地提高了工作效率，降低了包裝設計成本。但目前情況下，有限元法在紙類容器強度研究方面還不夠成熟，尤其是折疊紙盒抗壓強度的研究。由于受紙板原材料特性的制約，尚未有用于紙板壓縮應力分析評定的系統方法，這樣就不能區分出應力的類型，造成有限元法不能對應力進行進一步分析，得出的結論可能對紙盒結構的優化提供不了更加可信的科學依據，因此，這些方面還有待進一步的研究與發展。

總之，有限元法為包裝設計及研究人員提供了更為直觀更加快捷的研究手段，通過使用有限元分析的方法我們就能夠建立起紙盒的有限元模型并研究和分析它的力學特性。可以樂觀地估計，在不遠的將來，有限元方法將非常廣泛地應用到紙盒強度的研究領域，它將推動計算機輔助分析在包裝工程方面的應用向更高的水平發展。

參考文獻

[1]段瑞俠，劉雪瑩，陳金周.紙盒結構設計中要考慮的幾個要素[J].包裝工程，2008（12）.

[2]余本農，平幼妹等.關于折疊紙盒抗壓強度的討論[J].包裝工程，2002（1）.

[3]王金林.紙盒抗壓強度與白板紙挺度[J].包裝工程，1989（1）.

[4]HAKAN Grangard，JOSEF Kubat. Some Aspects of the Compressive Strength of Cartons[J].Svenak Papperstiding，1969（15）.

[5]劉慧，張新昌.折疊紙盒結構及其尺寸對抗壓強度的影響[J].包裝工程，2008（5）.

[6]張新昌，劉慧.折疊紙盒抗壓強度經驗計算公式的探討[J].包裝工程，2008（10）.

[7]袁毅，肖穎吹.折疊紙盒鎖底結構承載力實驗研究[J].包裝工程，2014（7）.

[8]李曉麗.蜂窩紙板靜態壓縮力學性能仿真研究[D].淮南：安徽理工大學，2011.